LeetCode

53. Maximum Subarray

文章目录
  1. 1. 题目
  2. 2. 思路

题目

https://leetcode.com/problems/maximum-subarray/

思路

这道题可以说是我这两天见过的最有趣的题了，表面上看起来非常简单，只有一脚踩进去才知道里面深千尺。最开始我完全找不到思路，于是开始看答案，第一眼看到的是这个：

看得心如死灰。

尝试了一下写遍历：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        max=nums[0]
        for i,num in enumerate (nums):
            sum = num
            if(sum>max):
                    max=sum
            for j in range(i+1,len(nums)):
                 sum=sum+nums[j]
                 if(sum>max):
                    max=sum
        return max

很显然这种东西怎么可能过得了…复杂度应该是O(n^2)

然后我找到了个魔法般的Kadane’s algorithm：https://www.youtube.com/watch?v=2MmGzdiKR9Y

这个视频很方便又简单地让我理解了动态规划在这道题的应用，代码如下 ：

1
2
3
4
5
6
7
8
class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        max_current = max_global = nums[0]
        for num in nums[1:]:
            max_current = max(num,max_current+num)
            if(max_current>max_global):
                max_global = max_current
        return max_global

这个视频最精髓的一部分我感觉应该在这里：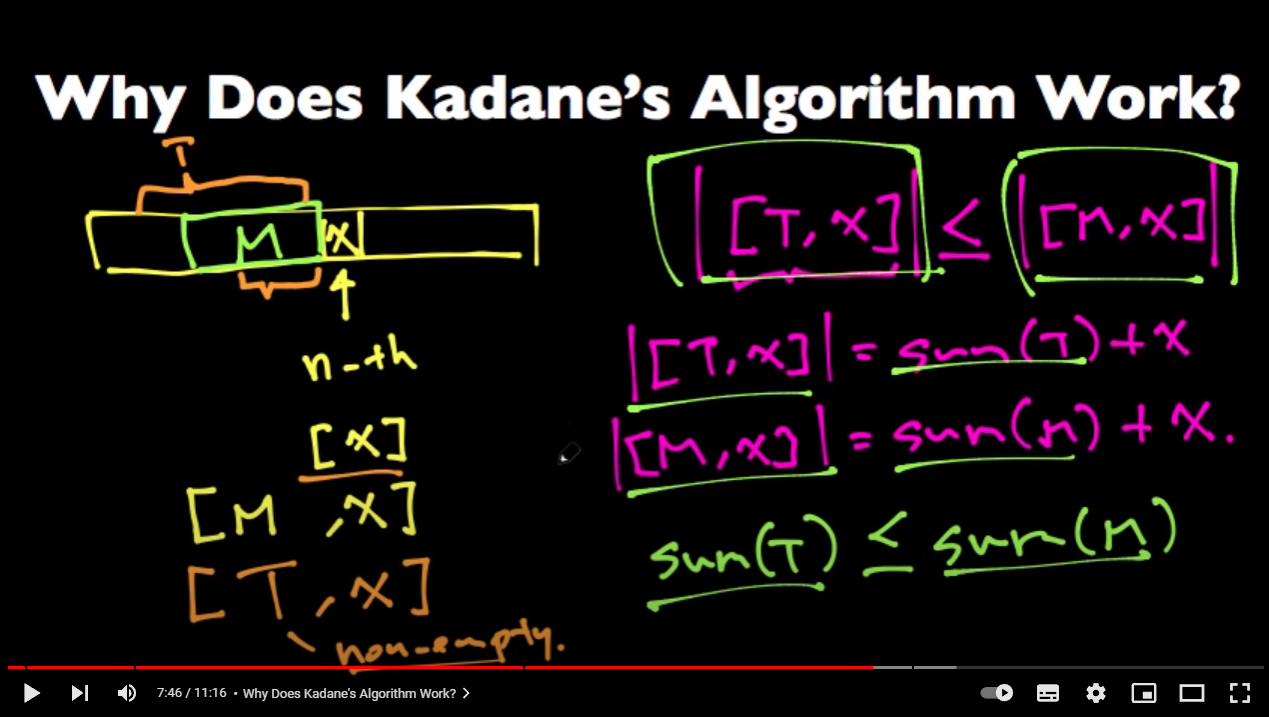

以当前位置为X，过去的状态为M，比对X+M与X之间的大小。这里作者还举例了，假设存在一个更大区间并且覆盖M范围的T，T与X比对，当T+X小于M+X的时候，则必然sum[M]大于sum[T]。

而视频最后直接使用例子来描述动态规划的本质：计算每个数值时候时候让计算结果能够保存在当前位置下的状态，例如max_current = max(num,max_current+num)，然后这些状态可以被利用起来计算之后的状态。

然后最后我看到了一个神来一手：

1
2
3
4
for i in range(1, len(nums)):
    if nums[i-1] > 0:
        nums[i] += nums[i-1]
return max(nums)

作者的原话是：

本质上和Kadane’s algorithm原理是一致的，同样是不断动态获取局部的最优解。但是简洁到让人难以想象。